top of page

MULTIPLE ROOTS
This method solve the problem that a derivative can be equal to zero in the Newton method, as this decreases the speed of convergence leads to a division by zero.
In the case that a root xv can be repeated multiple times on a function, which means it follows the expression , where m is the multiplicity and q ( x ) ≠ 0 , methods such as Newton and secant tend to fail. To solve these problems the following expression is proposed to calculate xn + 1 in the iterative system.
The convergence of this methos is cuadratic.
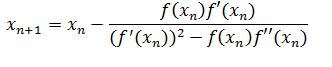

Information from:
bottom of page